

 Es 25 de diciembre. Se celebra en el Estadio Olímpico de Montreal un partido solidario en beneficio de los Matemáticos Incomprendidos.
Es 25 de diciembre. Se celebra en el Estadio Olímpico de Montreal un partido solidario en beneficio de los Matemáticos Incomprendidos.
La alineación de uno de los equipos está formada por los siguientes jugadores:
| Jugador | Edad |
|---|---|
| Manuel Neuer | 26 |
| Thomas Vermaelen | 27 |
| Daniel Agger | 28 |
| Fabio Coentrao | 24 |
| Yaroslav Rakitskiy | 23 |
| Jesús Navas | 26 |
| Samir Nasri | 25 |
| Urby Emanuelson | 26 |
| Theo Walcott | 23 |
| Mario Balotelli | 22 |
| Robert Lewandowski | 24 |

La media de edad del equipo es de 25 años exactos.
En el minuto 60, el entrenador decide sustituir a Nasri (25 años) por otro jugador.
Tras la sustitución, la media de edad ha subido 2 años.
¿Podrías calcular cuál es la edad del nuevo jugador?
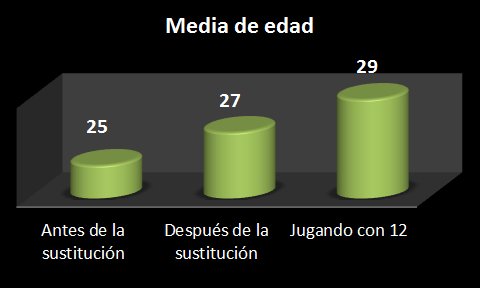
Tras este cambio, los entrenadores de ambos equipos deciden jugar el último cuarto de hora con 12 jugadores.
¿Qué edad deberá tener el nuevo jugadorque entra en el terreno de juego para que vuelva a subir la media otros 2 años más?

En el primer caso, para calcular la edad del jugador que saltará al terreno de juego para incrementar la edad media en dos años, el método más sencillo es el siguiente.
Sumaremos los años de todos los jugadores. Si la media es 25 años, y son 11 jugadores, multiplicaremos: 25 * 11 = 265 años.
Después de la sustitución, los jugadores sumarán un total de: 27 * 11 = 297 años.
Como hay una diferencia de 297 - 265 = 32 años, esto significa que el reserva que entra deberá tener 32 años más que el jugador al que va a sustituir, en este caso: 32 + 25 = 57 años
 ¡Un bonito regalo de Navidad para Rummenigge!
¡Un bonito regalo de Navidad para Rummenigge!
En el caso de que haya 12 jugadores sobre el terreno de juego, los cálculos serían los siguientes: primero hallamos el total de años antesdel cambio multiplicando 27 * 11 = 287 años
Total de años después del cambio: 29 * 12 = 348. Diferencia de años: 348 - 287 = 61 años. El jugador entrante deberá tener 61 años.
 ¡Otro regalo de Navidad, ahora para Johan Neeskens!
¡Otro regalo de Navidad, ahora para Johan Neeskens!
Hay veces que cuando entramos en un local donde, por ejemplo, se celebra un concurso de bailes de salón para mayores de 80 años, o una competición de juegos de videoconsolas para menores de 10 años, solemos decir: 'acabamos de subir/bajar la media de edad en 5 años'.
En realidad, controlamos intuitivamente el concepto de media de una forma relativamente correcta cuando se trata de manejar unos pocos valores, pero empezamos a perder la visión global de la misma conforme vamos incrementando la población que estudiamos.
Así, si nos atenemos al segundo caso, vamos a ver qué necesitamos para modificar la media de edad de un colectivo, cuando añadimos un elemento más al grupo.
Si llamamos x1,x2,...xn a las distintas edades de las personas que componen un grupo de n individuos, tendremos que su edad media será:
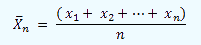
Si ahora añadimos una persona más (n+1), tendremos que su edad media será:
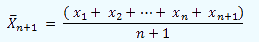
Si queremos que esta media varíe en un número 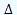 de años respecto a la media anterior, tendremos:
de años respecto a la media anterior, tendremos:
 de años respecto a la media anterior, tendremos:
de años respecto a la media anterior, tendremos: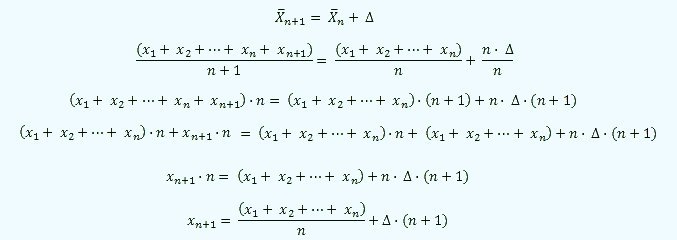
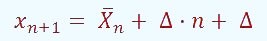
Así que por cada año (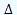 = 1) que deseemos incrementar la media de edad de una población, necesitamos introducir un individuo con una edad igual a la media anterior de edades más la cifra total de individuos más 1.
= 1) que deseemos incrementar la media de edad de una población, necesitamos introducir un individuo con una edad igual a la media anterior de edades más la cifra total de individuos más 1.
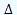 = 1) que deseemos incrementar la media de edad de una población, necesitamos introducir un individuo con una edad igual a la media anterior de edades más la cifra total de individuos más 1.
= 1) que deseemos incrementar la media de edad de una población, necesitamos introducir un individuo con una edad igual a la media anterior de edades más la cifra total de individuos más 1.
Evidentemente, cuanto mayor sea n, esto es, cuanto más individuos integren el grupo, más difícil será encontrar a alguien lo suficientemente mayor para aumentar dicha media.
Y análogamente, si queremos reducir la media en una unidad, (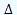 = -1), obtendremos que:
= -1), obtendremos que:
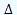 = -1), obtendremos que:
= -1), obtendremos que: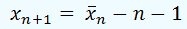
Lo cual quiere decir que si n es lo suficientemente grande, será imposible rebajar la media de edades en un año introduciendo sólo un individuo.
Así que la próxima vez que visitemos un concurso de bailes de salón o una competición de consolas de videojuegos, no deberemos sentirnos extraños entre dicho público, ya que la media de edades apenas si se resentirá por nuestra presencia...













